Dos Ecuaciones Lineales con Dos Incógnitas

Presentada la idea que nos motivará en la primer parte del estudio del álgebra lineal, volvemos a un sistema pequeño, de m y n conocidos. Empezaremos con un sistema de 2 ecuaciones con 2 incógnitas, llamado sistema de 2x2. El primer número indica la cantidad de ecuaciones, mientras el segundo número indica la cantidad de variables o incógnitas. Es decir, más adelante cuando generalicemos, trataremos con sistemas de mxn.

Escribiendo el sistema de 2x2, tenemos:

\begin{equation} \begin{aligned} a_{11} x + a_{12} y = b_1 \\ a_{21} x + a_{22} y = b_2 \end{aligned} \end{equation}

donde cada a_ij y b_i son números dados. Cada ecuación corresponde a una línea recta, y la solución del sistema es el (o los) par (o pares) de números (x,y) que satisface(n) ambas ecuaciones a la vez. En términos geométricos, la solución es (o son) el punto (o puntos) donde ambas rectas se intersectan. Es decir, el punto o los puntos en común que tienen ambas rectas.

Pensando en términos geométricos, pueden ocurrir 3 casos: Si las rectas se intersectan en un solo punto, hay solución única:

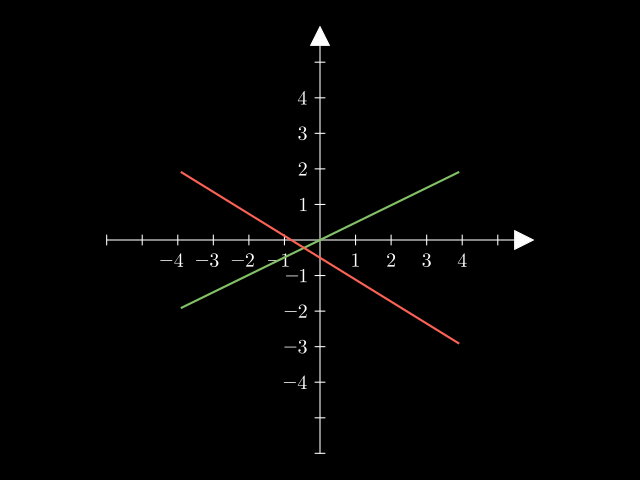
Si las rectas son paralelas y distintas, no hay solución:

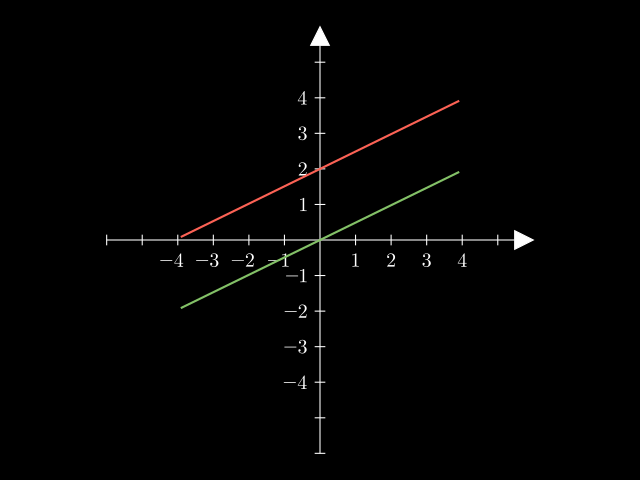
Y si las dos ecuaciones en sí refieren a la misma recta, hay un Número infinito de soluciones.

Tenemos entonces 3 posibilidades: O la solución es el conjunto vacío, o es un solo punto, o es en sí toda la recta.

Prestémosle atención al tercer caso: Quiere decir que una recta puede tener más de una ecuación, pero que no importa como la escribamos, siempre refieren a la misma recta. Es decir, si bien dos ecuaciones pueden aparentar representar dos rectas distintas, ya que los números no son idénticos, están de alguna manera relacionados entre sí y en realidad representan a la misma recta.

Cuando los sistemas tienen solución (sea única o sean infinitas), los llamamos consistentes o compatibles. Cuando no tienen solución, decimos que el sistema es inconsistente o incompatible. Dentro de los sistemas compatibles, si la solución es única decimos que es compatible determinado mientras que si tiene infinitas soluciones decimos que es compatible indeterminado.

Utilizaremos un procedimiento para resolver este sistema de 2x2, que luego intentaremos generalizar. Antes de dar el primer paso, nos quitaremos de encima algunos casos obvios, ya que hasta el momento no hemos puesto condiciones sobre los números a_ij.

Supondremos que a₁₂ no es 0, ya que si lo fuera, podríamos despejar x sencillamente de la primera ecuación y reemplazar ese valor en la segunda ecuación para encontrar el valor de y. Utilizando el mismo razonamiento, suponemos que a₂₂ es distinto de 0 también. O, por los mismos motivos, a₁₁ y a₂₁.

Ahora sí, comenzaremos con la técnica de eliminación, en el que haremos foco en eliminar el coeficiente a₂₁. Si multiplicamos la primer ecuación por a₂₁ y la segunda por a₁₁, obtenemos el siguiente sistema de ecuaciones, equivalente al inicial:

\begin{equation} \begin{aligned} a_{21}a_{11} x + a_{21}a_{12} y = a_{21}b_1 \\ a_{11}a_{21} x + a_{11}a_{22} y = a_{11}b_2 \end{aligned} \end{equation}

Equivalente significa que las soluciones (x,y) (si las hubiera) de este nuevo sistema son también soluciones del sistema original.

Ahora podemos restarle a la segunda ecuación la primera, obteniendo una tercera. Hacemos esto porque es la manera de eliminar el término en común a₂₁a₁₁x en ambas ecuaciones.

\begin{equation} \begin{aligned} (a_{11}a_{22} - a_{21}a_{12}) y = a_{11}b_2 - a_{21}b_1 \end{aligned} \end{equation}

Podemos despejar la variable y, entonces, ya que tenemos una sola incógnita en esta ecuación. Pero debemos prestar atención: solo podemos despejarla si el número dado por (a₁₁a₂₂ - a₂₁a₁₂) es distinto de 0. Siempre tenemos que estar atentos a que si pasamos un término dividiendo, éste sea distinto de cero.

\begin{equation} \begin{aligned} y = \frac{(a_{11}b_2 - a_{21}b_1)}{(a_{11}a_{22} - a_{21}a_{12})} \end{aligned} \end{equation}

Luego, con este valor de y podemos volver a la primer ecuación y encontrar el valor de x, resolviendo así el sistema.

\begin{equation} \begin{aligned} a_{11}x + a_{12}\frac{a_{11}b_2 - a_{21}b_1}{a_{11}a_{22}-a_{21}a_{12}} = b_1 \end{aligned} \end{equation} \begin{equation} \begin{aligned} x = \frac{1}{a_{11}} (b_1 - a_{12}\frac{a_{11}b_2 - a_{21}b_1}{a_{11}a_{22}-a_{21}a_{12}}) \end{aligned} \end{equation}

Esa es la resolución genérica del sistema de ecuaciones lineales de 2x2 planteado inicialmente. Muchas veces esa solución es todo lo que estamos buscando, pero en este curso queremos explorar que es lo que determina que un sistema tenga soluciones únicas. Así, volviendo a lo que hicimos hincapié, la única forma de que el sistema tenga una solución única es que

\begin{equation} \begin{aligned} a_{11}a_{22} - a_{21}a_{12} \ne 0 \end{aligned} \end{equation}

Cuando este número es 0, no tenemos información de si el sistema no tiene solución, o tiene soluciones infinitas. Pero en el caso de un sistema de 2x2, sabemos que las 2 ecuaciones pertenecen a dos rectas paralelas. Encontrando un punto de paso de una de las rectas, es decir, un par ordenado (x,y) que satisface una de las ecuaciones, podemos reemplazar ese par (x,y) en la otra ecuación y verificar si se satisface o no. Si se satisface, entonces ambas ecuaciones refieren a la misma recta (si dos rectas paralelas pasan por el mismo punto, entonces son la misma recta). Si no se satisface, entonces ambas rectas son paralelas y no coincidentes, por lo que el sistema no tiene solución.