Introducción
Este es un curso de álgebra lineal elemental. Lo más importante por el momento es que trataremos de generalizar propiedades de las líneas rectas, de ahí que usamos la palabra "lineal".
Decimos generalización porque tratamos de aplicar el conocimiento de resolución de sistemas de ecuaciones lineales no solo cuando están presentes dos variables, sino cuando hay un número m de ecuaciones y un número n de variables, cualesquiera sean los números enteros positivos m y n, no necesariamente iguales. Es decir, podremos tener 4 ecuaciones de 6 incógnitas, 2 ecuaciones de 2 incógnitas, 1 ecuación de 4 incógnitas, etc.
Si no recordás los distintos métodos para resolver sistemas de ecuaciones lineales de 2x2, entonces probablemente necesitás repasar la clase correspondiente: http://127.0.0.1:8000/courses/lessons/X.
1. Hechos Fundamentales de las Líneas Rectas
Como primera definición de línea recta, podemos decir que es un objeto que surge al unir 2 puntos en el plano mediante un trazo continuo, en una sola dirección. Debemos notar que como es un trazo continuo, está formada por infinitos puntos.
Las líneas rectas en el plano están descriptas por ecuaciones lineales de dos variables, que podemos escribir así:
\begin{equation} ax + by = c \end{equation}Donde a, b y c son constantes positivas y x, y son las variables, que geométricamente podemos tomar como los ejes cartesianos.
Entonces, dados 2 puntos cualquiera, P1 y P2, ubicados en cualquier lugar, podemos unirlos con una única línea recta: decimos que con 2 puntos, la recta queda "definida".
1.1. Propiedades
1.1.1. Pendiente
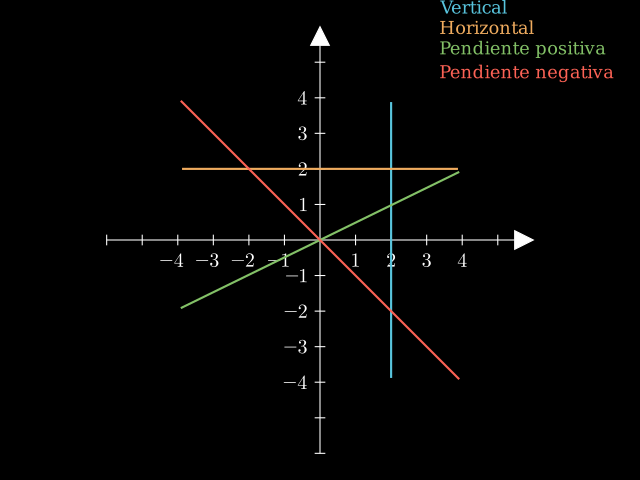
Es la inclinación que tiene la recta, respecto a un eje horizontal.
Hay rectas que son horizontales (no tienen inclinación, su pendiente
es cero), poca inclinación, mucha inclinación o son verticales
(tienen una pendiente indefinida, máxima).
Para calcular la pendiente de una recta conociendo dos puntos P1(x1,y1) y P2(x2,y2), podemos hacer:
\begin{equation} m = \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1} \end{equation}Es decir, estamos viendo cuánto cambia la variable y (hacia arriba o hacia abajo) cuando cambia la variable x.
Esto lo podemos hacer siempre que x1 ≠ x2, ya que de otra manera estaríamos dividiendo por cero, que no está definido. Por eso decimos que las rectas verticales tienen pendiente indefinida.
Otra cosa que debemos notar es que no importa cual punto elijamos como 1 y cual como 2, siempre que mantengamos el orden correcto en las restas. Es decir:
\begin{equation} m = \frac{y_2-y_1}{x_2-x_1} = \frac{y_1-y_2}{x_1-x_2} \end{equation}1.1.2. Ordenada al Origen
Cualquier recta que no sea vertical corta al eje
vertical y en un dado valor, al que llamamos "ordenada al origen".
La ordenada al origen puede ser positiva, negativa, o incluso cero,
que significa que la recta pasa por el origen, el punto (0,0).
1.2. Recta Horizontal
Una recta horizonal es paralela al eje x, y cumple con que si dos
puntos pertenecen a la recta, entonces y1 = y2. Su pendiente es
0, ya que:
1.3. Recta Vertical
Una recta vertical es paralela al eje y, y cumple con que si dos
puntos pertenecen a la recta, entonces x1 = x2. Su pendiente es
indefinida, ya que no podemos dividir por 0.
1.4. Rectas Paralelas
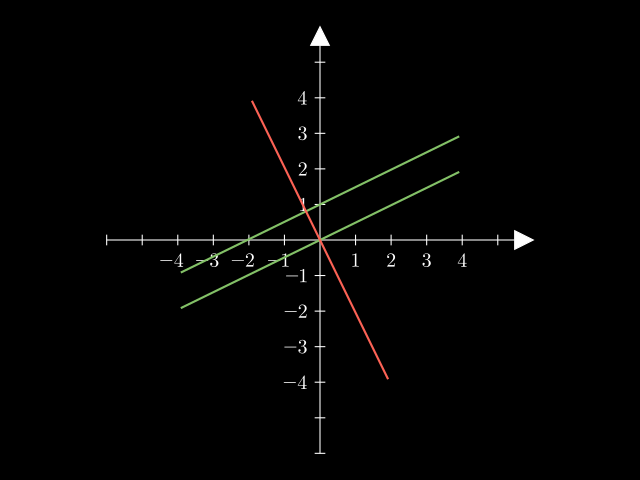
Dos rectas distintas son paralelas si y sólo si tienen la misma
pendiente, y distinta ordenada al origen. Si tienen la misma
pendiente y la misma ordenada al origen, entonces en realidad son la
misma recta.
1.5. Rectas Perpendiculares
Dos rectas son perpendiculares si se cumple una determinada relación
entre sus pendientes:
Esto es, las pendientes son opuestas (por eso el signo "-") y recíprocas (por eso el "1/"). Esto lo podemos interpretar con que si m1 es positiva y con poca pendiente, entonces la pendiente de la otra recta debe ser negativa y con mucha pendiente.
1.6. Ecuación General de la Recta
Trabajaremos con una forma en particular de escribir la ecuación de la
recta:
Y veamos ciertas condiciones sobre A y B:
1.6.1. Caso 1
Si A y B son 0, entonces sí o sí C = 0, que nos deja con una igualdad
que si bien es correcta, 0 = 0, no define una recta en sí.
1.6.2. Caso 2
Si A = 0, entonces:
que es la ecuación de una recta horizontal.
1.6.3. Caso 3
Si B = 0, entonces:
que es la ecuación de una recta vertical.
1.6.4. Caso 4
Si ni A ni B son 0, podemos escribir AB ≠ 0, y entonces, despejamos
y:
Demostraremos que la pendiente es -A/B y que la ordenada al origen es C/B.
Supongamos dos valores distintos de x, x1 y x2. Entonces:
\begin{equation} y_1 = \frac{C}{B}-\frac{A}{B}x_1 \end{equation} \begin{equation} y_2 = \frac{C}{B}-\frac{A}{B}x_2 \end{equation}Calculamos m:
\begin{equation} m = \frac{y_2-y_1}{x_2-x_1} = \frac{\frac{C}{B}-\frac{A}{B}x_2-(\frac{C}{B}-\frac{A}{B}x_1)}{x_2-x_1} \end{equation} \begin{equation} m = \frac{\frac{-A}{B}(x_2-x_1)}{x_2-x_1} = \frac{-A}{B} \end{equation}Por otro lado, para ver la ordenada al origen, forzamos a x a valer 0, y entonces:
\begin{equation} y = \frac{C}{B} - \frac{A}{B}*0 = \frac{C}{B} \end{equation}y ha quedado demostrado.
2. Las ecuaciones lineales. Propiedades
Volvamos entonces a la ecuación de la recta planteada anteriormente:
\begin{equation} ax + by = c \end{equation}Debemos observar que las dos variables aparecen con un exponente igual a 1 y se combinan mediante una operación de suma (o resta). Esta es la principal característica de las ecuaciones lineales. Es decir, por más que agreguemos variables hasta llegar a n variables (estamos generalizando), la forma en que las agregaremos será siempre con un exponente igual a 1, y combinándolas mediante sumas o restas. Para enfatizar este concepto, la siguiente no es una ecuación lineal:
\begin{equation} axy + y^2 + \frac{b}{x} = c \end{equation}Ahora bien, cuando tengamos n variables (y debemos recordar que n puede ser un número cualquiera, incluso muy grande), podríamos encontrarnos con el problema de no poder representar cada variable ni cada coeficiente con una letra, ya que las letras no son infinitas. Pero los números enteros sí son infinitos (y usaremos tanto el 0 como los números positivos), así que podemos usarlos como subíndices. Así, una ecuación de 5 variables la podemos expresar de la siguiente forma:
\begin{equation} a_1x_1 + a_2x_2 + a_3x_3 + a_4x_4 + a_5x_5 = b \end{equation}Y generalizando para n variables:
\begin{equation} a_1x_1 + a_2x_2 + ... + a_nx_n = b \end{equation}Podemos compactar aún más la notación utilizando el símbolo de la sumatoria:
\begin{equation} \sum_{i=1}^{n} a_ix_i = b \end{equation}3. Los sistemas de ecuaciones lineales
Tenemos un sistema de ecuaciones lineales cuando tenemos 2 o más ecuaciones lineales que están relacionadas entre sí. Es decir, cuando las variables representan la misma idea, concepto, cantidad física, etc. Volviendo a las ecuaciones de 2 variables, podríamos tener el siguiente sistema:
\begin{align} ax + by = c \\ dx + ey = f \end{align}Pensándolo geométricamente tenemos entonces dos rectas en el plano cartesiano.
Haciendo la misma consideración de que nos quedaríamos sin letras para cuando tengamos m ecuaciones con n incógnitas, podríamos emplear un nuevo subíndice para representar el número de la ecuación. Es decir:
\begin{align} a_{11}x_1 + a_{12}x_2 + ... + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + ... + a_{2n}x_n = b_2 \\ ... \\ a_{n1}x_1 + a_{n2}x_2 + ... + a_{nn}x_n = b_n \\ \end{align}Observamos que el primer subíndice refiere al número de ecuación (y tuvimos que agregárselo también a cada constante b, para distinguirlas) y que el segundo subíndice refiere al número de la variable con la que está relacionada. Por supuesto, esta forma de escribir sin separar los subíndices puede volverse ambigua cuando tenemos, por ejemplo, a211. ¿Es este el coeficiente 11 de la ecuación 2, o el coeficiente 21 de la ecuación 1? Cuando haya riesgo de confusión, habrá que separar los subíndices de alguna manera, por ejemplo con una coma: a2,11 no deja dudas que estamos hablando del coeficiente 11 de la ecuación 2.
Utilizando el símbolo de sumatoria, tenemos:
\begin{align} \sum_{i=1}^{n}a_{1i}x_i = b_1 \\ \sum_{i=1}^{n}a_{2i}x_i = b_2 \\ ... \\ \sum_{i=1}^{n}a_{ni}x_i = b_n \end{align}